|
Pour trier les données stockées dans un fichier, il est nécessaire de charger
celles-ci en mémoire (dans un tableau), d’en faire le tri suivant un ou plusieurs
critères, puis de réenregistrer le tableau dans le fichier.
Il existe plusieurs méthodes de tri (par sélection, par échange, etc.), leur
efficacité reposant sur la longueur et la complexité du programme et surtout
sur le temps d’éxecution. Les moins éfficaces nécessitent un temps proportionnel
au carré du nombre d’éléments à trier (N x N), les plus rapides à N x log(N).
Nous allons décrire trois méthodes dont vous pouvez comparer les performances :
TABLEAU COMPARATIF
| nb d’articles | 30 | 150 | 300 | 600 |
| Sélection | 3.9s | 79s | 295s | |
| Dichotomie | 3.9s | 55s | 194s | |
| Shell-Metzner | 1.7s | 18s | 33.8s | 86s |
| Arborescence | 1.7s | 17s | 38s | 100s |
TRI PAR SELECTION
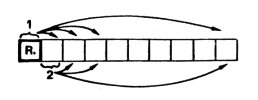
Dans cette méthode, on prend un élément de référence. On le compare successivement
à chacun de ses suivants. Si l’élément de référence est plus petit, c’est bon.
Sinon, on l’échange avec le suivant concerné. Arrivé au dernier suivant,
l’élément de référence contient le plus petit élément du tableau. On prend alors
son suivant comme référence et ce jusqu’au dernier.
Cette méthode, facile à programmer, ne peut être utilisée que pour de petits fichiers.
Exemple de code
10 REM TRI PAR SELECTION
20 REM DU TABLEAU D$
30 FOR I=1 TO M-1
40 FOR J=I+1 TO M
50 IF D$(J) < D$(I) THEN AA$ = D$(J) : D$(J) = D$(I) : D$(I) = AA$
60 NEXT J
70 NEXT I
80 RETURN
TRI PAR DICHOTOMIE
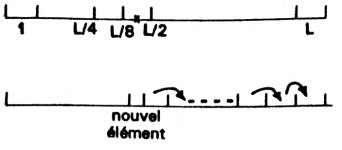
Le principe est le suivant : On considère que N éléments sont rangés dans
l’ordre voulu (croissant pour l’exemple). On souhaite insérer un nouvel élément.
Pour cela, nous prenons l’élément du milieu et nous le comparons à l’élément
nouveau. Si le nouvel élément est plus petit, sa place sera dans le sous-ensemble
gauche, sinon dans le sous-ensemble droit. On recommence l’algorithme jusqu’à ce
que la gamme couverte par le sous-ensemble corresponde à 1. Nous connaissons
alors la place à laquelle il faut ranger le nouvel élément. Nous devrons alors
décaler tous les éléments qui suivent d’une position et ranger dans la place
libérée le nouvel élément.
Exemple de code
10 REM TRI PAR DICHOTOMIE
20 REM DU TABLEAU D$
30 IF D$(1) > D$(2) THEN AA$ = D$(2) : D$(2) = D$(1) : D$(1) = AA$ : GOTO 40
40 FOR N=3 TO M
50 R=0 : D=N : G=0 : Z=D-G : C=1
60 E = INT(Z/2)
70 R = R+E*C
80 IF D$(N) < D$(R) THEN D=R : C=-1 : GOTO 100
90 G=R : C=1
100 Z=D-G : IF Z>1 THEN GOTO 60
110 IF C=1 THEN R=R+1
120 AA$ = D$(N)
130 FOR I=N TO 1 STEP -1
140 IF R=I THEN D$(I)=AA$ : GOTO 160
150 D$(I)=D$(I-1) : NEXT I
160 NEXT N
170 RETURN
TRI PAR LA METHODE SHELL-METZNER
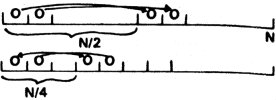
L’ensemble des données est successivement décomposé en sous-ensembles
de plus en plus petits (divisé par deux à chaque itération). Un élément
d’un sous-ensemble est alors comparé à son correspondant du sous-ensemble
suivant, avec échange s’il y a lieu et, dans ce cas, on remonte au
sous-ensemble précédent pour remise en ordre éventuelle et ainsi de suite
jusqu’à premier sous-ensemble. Le travail est terminé lorsque le
sous-ensemble ne comporte plus qu’un élément.
Par cette méthode, le ne élément d’un sous-ensemble est toujours
inférieur au ne élément du sous-ensemble suivant.
Pour utiliser cet algorithme pour faire un tri, il suffit de ranger
les deux premiers éléments. On insère ensuite chacun des éléments de la
suite en appliquant la procédure décrite.
Cette méthode est évidemment plus éfficace que la précédente, mais elle
reste largement insuffisante lorsque le fichier dépasse une centaine
d’articles.
Le
tri par cette méthode est efficace et le programme, écrit en Basic,
prend peu de place. Pour un tableau de 300 éléments, la méthode de
Shell-Metzner est 6 fois plus rapide que la méthode par Dichotomie !
Exemple de code
10 REM TRI PAR SHELL-METZNER
20 REM DU TABLEAU D$
30 P=M
40 P=INT(P/2)
50 IF P<1 THEN RETURN
60 DEB=1 : FIN=M-P
70 R=DEB
80 C=R+P : IF D$(R)<=D$(C) GOTO 100
90 AA$=D$(R) : D$(R)=D$(C) : D$(C)=AA$ : R=R-P : IF R>0 GOTO 80
100 DEB=DEB+1 IF DEB>FIN THEN GOTO 40 ELSE GOTO 70
110 RETURN
Exemple :
TRI PAR ARBORESCENCE
Le tri par arborescence découle directement de la théorie des graphes
dont nous rappelons quelques notions :
- Un graphe est composé de sommets et d’arcs les reliant.
- Une arborescence est un arbre dont chaque sommet (à l’exception du
plus haut appelé racine) est l’extrémité terminale d’un seul arc.
- Un noeud est un sommet qui est l’origine d’au moins un arc
vers un sommet inférieur.
- Les feuilles sont les derniers sommets qui ne dépendent d’aucun
autre sommet.
Le tri par arborescence consiste à transformer la suite des
informations du tableau à trier en une structure arboresente en générant
les pointeurs de gauche, de droite et de sommet. Il comporte deux parties :
Dans le programme, nous utiliserons troix tableaux :
- D$() le tableau à trier (alpha-numérique dans notre cas),
- R$() le tableau de résultats.
- G() contiendra les pointeurs de gauche de l’élément.
- D() contiendra les pointeurs de droite de l’élément.
- PER() contiendra les pointeurs de sommet de l’élément.
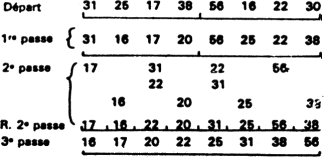
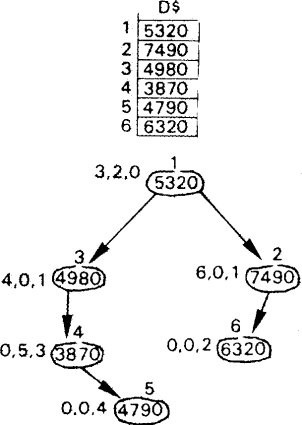
Exemple : soit trier le tableau de la figure.
Supposons que les 4 premiers éléments soient rangés en arborescence
et proposons de ranger les deux suivants.
Ajoutons 4790
4790 est comparé à la racine 5320, il est plus petit et le pointeur
gauche est non nul, on descend à gauche.
4790 est comparé à 4980, il est plus petit et le pointeur gauche
est non nul, on descend à gauche.
4790 est comparé à 3870, il est plus grand et le pointeur droit est
nul, on le met donc à droite.
Exemple de code
500 REM TRI PAR ARBORENSCENCE
510 REM DU TABLEAU D$
520 REM AVEC RESULTAT DANS R$
530 REM G() TABLEAU POINTEUR DE GAUCHE
540 REM D() TABLEAU POINTEUR DE DROITE
550 REM PER() TABLEAU POINTEUR DE SOMMET
560 REM EC$ ELEMENT COURANT
570 REM ER$ ELEMENT DE REFERENCE
580 PRINT "N=" ; N
590 DIM G(N), D(N), PER(N), R$(N)
600 FOR I=2 TO N
610 EC$=D$(I) : NR=1
620 ER$=D$(NR)
630 IF EC$<=ER$ GOTO 660
640 IF D(NR)<>0 THEN NR=D(NR) : GOTO 620
650 D(NR)=I : PER(I)=NR : GOTO 680
660 IF G(NR)<>0 THEN NR=G(NR) : GOTO 620
670 G(NR)=I : PER(I)=NR
680 NEXT I
690 I1=1 : J1=1
700 IF G(I1)=N+1 THEN I1=PER(I1) : GOTO 700
710 IF G(I1)<>0 THEN I1=G(I1) : GOTO 700
720 R$(J1)=D$(I1) : G(I1)=N
+1
730 J1=J1+1
740 IF J1=N+1 THEN RETURN
750 I2=PER(I1)
760 IF I2=0 OR G(I2)=N+1 THEN GOTO 780
770 G(I2)=0
780 IF D(I1)=0 OR D(I1)=N+1 THEN I1=PER(I1) : GOTO 700
790 I3=D(I1) : D(I1)=N+1 : I1=I3
800 GOTO 700
|